Line Intensity Scanning

The line intensity scan function is a graphical tool that is useful for measuring intensity and contrast along a single horizontal or vertical row of pixels in digital images. This technique is often employed to compare brightness values in related digital images, and to determine the average values over several adjacent pixel rows in a single image.

This interactive tutorial explores the line intensity scan technique for measuring intensity levels in blocks of up to seven pixels in a digital image. The tutorial initializes with a randomly selected specimen image (captured in the microscope) appearing in the left-hand window entitled Specimen Image. Each specimen name includes, in parentheses, an abbreviation designating the contrast mechanism employed in obtaining the image. The following nomenclature is used: (FL), fluorescence; (BF), brightfield; (DF), darkfield; (PC), phase contrast; (DIC), differential interference contrast (Nomarski); (HMC), Hoffman modulation contrast; and (POL), polarized light. Visitors will note that specimens captured using the various techniques available in optical microscopy behave differently during image processing in the tutorial.

Appearing to the right of the Specimen Image window is the Intensity Scan Profile window, which displays a graph of Scan Position versus Intensity for each column of pixels lying underneath the white horizontal scan line traversing the Specimen Image window. To operate the tutorial, select an image from the Choose A Specimen pull-down menu, and use the mouse cursor to drag the intensity scan line up and down over the display in the Specimen Image window. The white horizontal scan line can be repositioned vertically by either clicking inside the window, or dragging the line with the mouse to the desired location. Alternatively, the Scan Line Position slider can be employed to translate the line across the image surface. The Scan Line Width slider controls the width of the horizontal scan line, which has a range of one to seven pixels. If the scan line width is set to a value greater than one pixel, then the intensity value corresponding to each horizontal position on the scan line is computed as the arithmetic mean of the intensity values of all of the pixels in the column. Visitors should examine the appearance of the line intensity scan graph while positioning the scan line at various heights and varying the width of the horizontal scan line.

The line intensity scan function consists of a graph of pixel intensity values measured at each position along a horizontal (or vertical) scan line through a digital image. Relative height differences between points on the graph correspond to brightness differences between objects in the image. By comparing the height differences of various points on the graph, useful information regarding local and global image contrast can be obtained. A numerical representation of intensity values can also be obtained from the graph by applying a scale to the intensity axis. Intensity levels can be quantitatively measured to compare the overall intensity of one image to that of another. The accuracy of the intensity measured along the scan line can often be improved by increasing the line width so that it covers more than one horizontal line in the image. This maneuver has the general effect of reducing sharp spikes in the intensity scan profile, which results in a smoother graph. For a color digital image, a line intensity scan of the red, green, and blue color channels can be produced when the image is stored in the RGB color model. Similarly, a line intensity scan of an image can also be produced when it is stored in the HSI (Hue, Saturation, Intensity) color model. In the tutorial, three options including grayscale, RGB, and HSI line intensity scans are available.

In many cases, it is useful to relate pixel brightness information to other types of information contained in a digital image. The ratio of intensities at two or more wavelengths, computed for a single pixel or a region of interest, can yield valuable information about the specimen. Gray-level changes in single-wavelength images of fluorescently labeled cells are very difficult to interpret, because variations in the intensity of the peak absorption or emission signals of intracellular fluorescent dyes may be due to differences in local dye concentration, photon statistical noise, fluctuations in the excitation light intensity, or variations in detector gain. Ratio imaging alleviates many of these difficulties by making two measurements of the gray levels at the same spatial location in the image. Ratio imaging is a valuable tool in video microscopy of living cells for studies of cellular calcium transport. Calcium-sensitive fluorescent dyes emit a specific wavelength of light upon binding to a substrate. Two images of the living cell containing the fluorescent dye are captured, one at the characteristic emission wavelength for binding (sensitive) and the other at a reference wavelength (unbound). By comparing gray-level changes at the same location under different wavelengths, ratio imaging allows detection of calcium transport and binding sites in living cells with relatively short optical path lengths (a few micrometers).

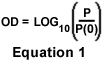
Many compounds absorb ultraviolet or visible light. Beer's Law (A = εCL) expresses the absorption of light (A) transmitted through a chemical solution as the product of the extinction coefficient of the compound (ε), the optical path length (L) of the sample, and the concentration (C) of the compound in the solution. Optical density, defined in Equation 1, is an expression of the logarithmic ratio of the intensity of light incident on a specimen (P(0)) to the intensity of light passing through it (P). Since absorption can be expressed as the reciprocal of optical density (A = 1 / OD), Beer's law states that a clear relationship exists between transmission of light through the specimen solution and the concentration of the chemical compound it contains. Thus, if a sample solution of a drug is tagged with fluorescent dyes and a grayscale image of the sample is captured with a properly calibrated camera, the dosage of the drug and the fading rate of the fluorescent dyes can be determined.