Microscope Objectives Introduction
Microscope objectives are perhaps the most important components of an optical microscope because they are responsible for primary image formation and play a central role in determining the quality of images that the microscope is capable of producing. Objectives are also instrumental in determining the magnification of a particular specimen and the resolution under which fine specimen detail can be observed in the microscope.
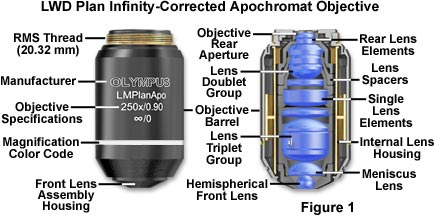
The objective is the most difficult component of an optical microscope to design and assemble, and is the first component that light encounters as it proceeds from the specimen to the image plane. Objectives derive their name from the fact that they are, by proximity, the closest component to the object (specimen) being imaged.
Major microscope manufacturers offer a wide range of objective designs, which feature excellent optical characteristics under a wide spectrum of illumination conditions and provide various degrees of correction for the primary optical aberrations. The objective illustrated in Figure 1 is a 250x long working distance apochromat, which contains 14 optical elements that are cemented together into three groups of lens doublets, a lens triplet group, and three individual internal single-element lenses. The objective also has a hemispherical front lens and a meniscus second lens, which work synchronously to assist in capturing light rays at high numerical aperture with a minimum of spherical aberration. Although not present on this objective, many high magnification objectives of similar design are equipped with a spring-loaded retractable nosecone assembly that protects the front lens elements and the specimen from collision damage. Internal lens elements are carefully oriented and tightly packed into a tubular brass housing that is encapsulated by the objective barrel. Specific objective parameters such as numerical aperture, magnification, optical tube length, degree of aberration correction, and other important characteristics are imprinted or engraved on the external portion of the barrel. Although the objective featured in Figure 1 is designed to operate utilizing air as the imaging medium between the objective front lens and specimen, other objectives have front lens elements that allow them to be immersed in water, glycerin, or a specialized hydrocarbon-based oil.
Modern objectives, composed up of numerous internal glass lens elements, have reached a high state of quality and performance, with the extent of correction for aberrations and flatness of field determining the usefulness and cost of an objective. Construction techniques and materials used to manufacture objectives have greatly improved over the course of the past 100 years. Today, objectives are designed with the assistance of Computer-Aided-Design (CAD) systems using advanced rare-element glass formulations of uniform composition and quality having highly specific refractive indices. The enhanced performance that is demonstrated using these advanced techniques has allowed manufacturers to produce objectives that are very low in dispersion and corrected for most of the common optical artifacts such as coma, astigmatism, geometrical distortion, field curvature, spherical and chromatic aberration. Not only are microscope objectives now corrected for more aberrations over wider fields, but image flare has been dramatically reduced with a substantial increase in light transmission, yielding images that are remarkably bright, sharp, and crisp.
Three critical design characteristics of the objective set the ultimate resolution limit of the microscope. These include the wavelength of light used to illuminate the specimen, the angular aperture of the light cone captured by the objective, and the refractive index in the object space between the objective front lens and the specimen. Resolution for a diffraction-limited optical microscope can be described as the minimum detectable distance between two closely spaced specimen points:
where R is the separation distance, λ is the illumination wavelength, n is the imaging medium refractive index, and θ is one-half of the objective angular aperture. In examining the equation, it becomes apparent that resolution is directly proportional to the illumination wavelength. The human eye responds to the wavelength region between 400 and 700 nanometers, which represents the visible light spectrum that is utilized for a majority of microscope observations. Resolution is also dependent upon the refractive index of the imaging medium and the objective angular aperture. Objectives are designed to image specimens either with air or a medium of higher refractive index between the front lens and the specimen. The field of view is often quite limited, and the front lens element of the objective is placed close to the specimen with which it must lie in optical contact. A gain in resolution by a factor of approximately 1.5 is attained when immersion oil is substituted for air as the imaging medium.
The last, but perhaps most important, factor in determining the resolution of an objective is the angular aperture, which has a practical upper limit of about 72 degrees (with a sine value of 0.95). When combined with refractive index, the product:
is known as the numerical aperture (abbreviated NA), and provides a convenient indicator of the resolution for any particular objective. Numerical aperture is generally the most important design criteria (other than optical correction) to consider when selecting a microscope objective. Values range from 0.1 for very low magnification objectives (1x to 4x) to as much as 1.6 for high-performance objectives utilizing specialized immersion oils. As numerical aperture values increase for a series of objectives of the same magnification, we generally observe a greater light-gathering ability and increase in resolution. The microscopist should carefully choose the objective magnification, so that, under the best circumstances, detail that is just resolved should be enlarged sufficiently to be viewed with comfort, but not to the point that empty magnification hampers observation of fine specimen detail.
Just as the brightness of illumination in a microscope is governed by the square of the working numerical aperture of the condenser, the brightness of an image produced by the objective is determined by the square of its numerical aperture. In addition, objective magnification also plays a role in determining image brightness, which is inversely proportional to the square of the lateral magnification. The square of the numerical aperture/magnification ratio expresses the light-gathering power of the objective when utilized with transmitted illumination. Because high numerical aperture objectives are often better corrected for aberration, they also collect more light and produce a brighter, more corrected image that is highly resolved. It should be noted that image brightness decreases rapidly as the magnification increases. In cases where the light level is a limiting factor, choose an objective with the highest numerical aperture, but having the lowest magnification factor capable of producing adequate resolution.
The least expensive (and most common) objectives, employed on a majority of laboratory microscopes, are the achromatic objectives. These objectives are corrected for axial chromatic aberration in two wavelengths (blue and red; about 486 and 656 nanometers, respectively), which are brought into a single common focal point. Furthermore, achromatic objectives are corrected for spherical aberration in the color green (546 nanometers; see Table 1). The limited correction of achromatic objectives can lead to substantial artifacts when specimens are examined and imaged with color microscopy and photomicrography. If focus is chosen in the green region of the spectrum, images will have a reddish-magenta halo (often termed residual color). Achromatic objectives yield their best results with light passed through a green filter (often an interference filter) and using black and white film when these objectives are employed for photomicrography. The lack of correction for flatness of field (or field curvature) further hampers achromat objectives. In the past few years, most manufacturers have begun providing flat-field corrections for achromat objectives and have given these corrected objectives the name of planachromats.
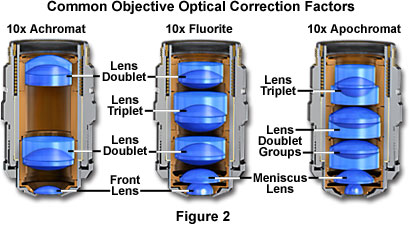
The next higher level of correction and cost is found in objectives called fluorites or semi-apochromats (illustrated by center objective in Figure 2), named for the mineral fluorite, which was originally used in their construction. Figure 2 depicts the three major classes of objectives: The achromats with the least amount of correction, as discussed above; the fluorites (or semi-apochromats) that have additional spherical corrections; and, the apochromats that are the most highly corrected objectives available. The objective positioned on the far left in Figure 2 is a 10x achromat, which contains two internal lens doublets and a front lens element. Illustrated in the center of Figure 2 is a 10x fluorite objective having several lens groups including two doublets and a triplet, in addition to a hemispherical front lens and a secondary meniscus lens. On the right in Figure 2 is a 10x apochromat objective that also contains multiple lens groups and single elements. Although similar in construction to fluorite objectives, the lenses have different curvatures and thickness, and are arranged in a configuration that is unique to apochromat objectives.
Objective Correction for Optical Aberration
| Objective Type |
Spherical Aberration |
Chromatic Aberration |
Field Curvature |
|---|---|---|---|
| Achromat | 1 Color | 2 Colors | No |
| Plan Achromat | 1 Color | 2 Colors | Yes |
| Fluorite | 2-3 Colors | 2-3 Colors | No |
| Plan Fluorite | 3-4 Colors | 2-4 Colors | Yes |
| Plan Apochromat | 3-4 Colors | 4-5 Colors | Yes |
Table 1
During assembly of the objective, lenses are first strategically spaced and lap-seated into cell mounts, then packaged into a central sleeve cylinder that is mounted internally within the objective barrel. Individual lenses are seated against a brass shoulder mount with the lens spinning in a precise lathe chuck, followed by burnishing with a thin rim of metal that locks the lens (or lens group) into place. Spherical aberration is corrected by selecting the optimum set of spacers to fit between the lower two lens mounts (the hemispherical and meniscus lens). The objective is made parfocal by translating the entire lens cluster upward or downward within the sleeve with locking nuts so that objectives housed on a multiple nosepiece can be interchanged without losing focus. Adjustment for coma is accomplished with three centering screws that can optimize the position of internal lens groups with respect to the optical axis of the objective.
Fluorite objectives are produced from advanced glass formulations that contain materials such as fluorspar or newer synthetic substitutes. These new formulations allow for greatly improved correction of optical aberration. Similar to the achromats, the fluorite objectives are also corrected chromatically for red and blue light. In addition, the fluorites are also corrected spherically for two or three colors instead of a single color, as are achromats. The superior correction of fluorite objectives compared to achromats enables these objectives to be made with a higher numerical aperture, resulting in brighter images. Fluorite objectives also have better resolving power than achromats and provide a higher degree of contrast, making them better suited than achromats for color photomicrography in white light.
Numerical Aperture

Investigate how the size of the light cone entering the objective front lens changes with the objective numerical aperture value.
Start Tutorial »
The highest level of correction (and expense) is found in apochromatic objectives, illustrated in Figures 2 and 3. Apochromats represent the most highly corrected microscope lenses currently available, and their high price reflects the sophisticated design and careful assembly required in their manufacture. In Figure 3, we compare lens elements in a series of apochromatic objectives ranging from 10x to 100x in magnification. The lower power apochromat objectives (10x and 20x) have a longer working distance and the overall objective length is shorter than in higher power (40x and 100x) apochromat objectives. Traditionally, apochromats are corrected chromatically for three colors (red, green, and blue), almost eliminating chromatic aberration, and are corrected spherically for either two or three wavelengths (see Table 1). Apochromatic objectives are the best choice for color photomicrography in white light. Because of their high level of correction, apochromat objectives usually have, for a given magnification, higher numerical apertures than do achromats or fluorites. Many of the newer high-performance fluorite and apochromat objectives are corrected for four (dark blue, blue, green, and red) or more colors chromatically and four colors spherically.

All three types of objectives suffer from pronounced field curvature and project images that are curved rather than flat, an artifact that increases in severity with higher magnification. To overcome this inherent condition arising from curved lens surfaces, optical designers have produced flat-field corrected objectives, which yield images that are in common focus throughout the viewfield. Objectives that have flat-field correction and low distortion are called planachromats, planfluorites, or planapochromats, depending upon their degree of residual aberration. Such correction, although expensive, is quite valuable in digital imaging and conventional photomicrography.
Field Curvature

A simple lens focuses image points from an extended flat object, such as a specimen on a microscope slide, onto a spherical surface resembling a curved bowl. Explore how field curvature aberrations degrade images observed in the microscope.
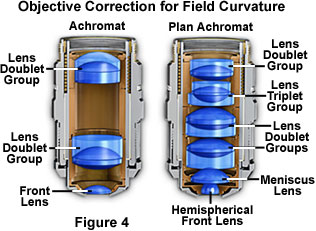
Start Tutorial »Uncorrected field curvature is the most severe optical aberration that occurs in fluorite (semi-apochromat) and apochromat objectives, and it was tolerated as an unavoidable artifact for many years. During routine use, the viewfield would have to be continuously refocused between the center and the edges to capture all specimen details. The introduction of flat-field (plan) correction to objectives perfected their use for photomicrography and video microscopy, and today these corrections are standard in both general use and high-performance objectives. Correction for field curvature adds a considerable number of lens elements to the objective as illustrated in Figure 4 with a simple achromat. The uncorrected achromat on the left in Figure 4 contains two lens doublets, in addition to a simple thin-lens front element. In contrast, the corrected plan achromat on the right in Figure 4 contains three lens doublets, a central lens triplet group, and a meniscus lens positioned behind the hemispherical front lens. Plan correction, in this instance, has led to the addition of six lens elements bundled into more sophisticated lens groupings, which dramatically increases the optical complexity of the objective. The significant increase in lens elements for plan correction also occurs with fluorite and apochromat objectives, frequently resulting in an extremely tight fit of lens elements (see Figure 1) within the internal objective sleeve. In general, plan objectives corrected for field curvature sacrifice a considerable amount of free working distance, and many of the high-magnification versions have a concave front lens, which can be extremely difficult to clean and maintain.
Older objectives generally have lower numerical apertures, and are subject to an aberration termed chromatic difference of magnification that requires correction by the use of specially designed compensating oculars or eyepieces. This type of correction was prevalent during the reign of fixed tube length microscopes, but is not necessary with modern infinity-corrected objectives and microscopes. In recent years, modern microscope objectives have their correction for chromatic difference of magnification either built into the objectives themselves (Olympus and Nikon) or corrected in the tube lens (Leica and Zeiss).
The intermediate image in an infinity-corrected system appears at the reference focal length (formerly, the optical tube length) behind the tube lens in the optical pathway. This length varies between 160 and 250 millimeters, depending upon design constraints imposed by the manufacturer. The magnification of an infinity-corrected objective is calculated by dividing the reference focal length by the focal length of the objective lens.
In most biological and petrographic applications, a cover glass is utilized in mounting the specimen, both to protect the integrity of the specimen and to provide a clear window for observation. The cover glass acts to converge the light cones originating from each point in the specimen, but also introduces chromatic and spherical aberration (and consequent loss of contrast) that must be corrected by the objective. The degree to which light rays are converged is determined by the refractive index, dispersion, and thickness of the cover glass. Although the refractive index should be relatively constant within a batch of cover glasses, the thickness can vary between 0.13 and 0.22 millimeters. Another concern is the aqueous solvent or excess mounting medium that lies between the specimen and cover glass in wet or thickly mounted preparations. For example, in physiological saline whose refractive index is significantly different from that of the coverslip, the objective must focus through a layer of water only a few microns thick, leading to significant aberrations and a deviation of the point spread function that is no longer symmetrical above and below the focal plane. These factors add to the effective variations in refractive index and thickness of the coverslip and are very difficult for the microscopist to control.
The imaging medium between the objective front lens and the specimen coverslip is also very important with respect to correction for spherical aberration and coma in the design of lens elements for objectives. Lower power objectives have relatively low numerical apertures and are designed to be used dry with only air as the imaging medium between the objective front lens and the cover glass. The maximum theoretical numerical aperture obtainable with air is 1.0, however in practice it is virtually impossible to produce a dry objective with a numerical aperture above 0.95. The effect of cover glass thickness variation is negligible for dry objectives having numerical apertures less than 0.4, but such deviation becomes significant at numerical apertures exceeding 0.65, where fluctuations as small as 0.01 millimeter can introduce spherical aberration. This poses problems with high-power apochromats, which must use very short working distances in air and contain sensitive corrections for spherical aberration that tend to make it difficult to obtain sharp images.
Cover Glass Correction

Investigate how internal lens elements in a high numerical aperture dry objective may be adjusted to correct for fluctuations in cover glass thickness.
Start Tutorial »To remedy this, many high-performance apochromat dry objectives are fitted with correction collars, which allow adjustment to correct for spherical aberration by correcting for variations in cover glass thickness (see Figure 5). Optical correction for spherical aberration is produced by rotating the collar, which causes two of the lens element groups in the objective to move either closer together or farther apart. The objective on the left in Figure 5 has had the correction collar adjusted for a cover glass thickness of 0.20 mm by bringing the adjustable lens elements very close together. In contrast, the objective on the right in Figure 5 has the adjustable lens elements separated by a rather large distance to compensate for very thin cover glasses (0.13 mm). A majority of the correction collar objectives designed for upright transmitted light microscopy have an adjustment range for cover glass thickness variations between 0.10 and 0.23 millimeters. Many of the specialized phase contrast objectives designed for observing tissue culture specimens with an inverted microscope have an even broader compensation range of 0 to 2 millimeters. This allows specimens to be viewed through the bottom of most culture vessels, which often have dramatic thickness fluctuations in this size range. Uncovered specimens, such as blood smears, can also be observed with correction collar objectives when the adjustment is set to 0 to account for the lack of a cover glass.
High numerical aperture dry objectives lacking a correction collar often produce images that are inferior to those of lower numerical aperture objectives where cover glass thickness is of less concern. For this reason, it is often prudent to choose a lower magnification (and numerical aperture) objective in order to obtain superior contrast without the accompanying artifacts introduced by cover glass fluctuations. As an example, a 40x objective having a numerical aperture of 0.65 may be able to produce better images with sharper contrast and clarity than a 60x-0.85 numerical aperture objective, even though the resolving power of the higher magnification objective is theoretically greater.

The standard thickness for cover glasses is 0.17 millimeters, which is designated as a number 1½ cover glass. Unfortunately, not all 1½ cover glasses are manufactured to this close tolerance (they range from 0.16 to 0.19 millimeters) and many specimens have media between them and the cover glass. Compensation for cover glass thickness can be accomplished by adjusting the mechanical tube length of the microscope, or (as previously discussed) by the utilization of specialized correction collars that change the spacing between critical elements inside the objective barrel. The correction collar is utilized to adjust for these subtle differences to ensure the optimum objective performance. Proper utilization of objective lenses with correction collars demands that the microscopist is experienced and alert enough to reset the collar using appropriate image criteria. In most cases, focus may shift and the image may wander during adjustment of the correction collar. Use the steps listed below to make small incremental adjustments to an objective's correction collar while observing changes in the specimen image.
- Position the correction collar so that the indicator mark on the objective barrel coincides with the 0.17 millimeter scale mark engraved on the collar housing.
- Place a specimen on the stage and focus the microscope on a small specimen feature.
- Rotate the correction collar very slightly and re-focus the objective to determine if the image has improved or degraded. Due to the fact that most specimen preparations suffer from cover glass/media sandwiches that are too thick, start the rotation experiment by trying larger compensation values (0.18-0.23) first.
- Repeat the previous step to determine if the image is improving or degrading as the correction collar is turned in a single direction.
- If the image has degraded, follow the same steps and rotate the correction collar in the opposite direction (toward lower values) to find the position offering optimum resolution and contrast.
Objective numerical aperture can be dramatically increased by designing the objective to be used with an immersion medium, such as oil, glycerin, or water. By using an immersion medium with a refractive index similar to that of the glass coverslip, image degradation due to thickness variations of the cover glass are practically eliminated whereby rays of wide obliquity no longer undergo refraction and are more readily grasped by the objective. Typical immersion oils have a refractive index of 1.51 and a dispersion similar to that of glass coverslips. Light rays passing through the specimen encounter a homogeneous medium between the coverslip and immersion oil and are not refracted as they enter the lens, but only as they leave its upper surface. It follows that if the specimen is placed at the aplanatic point (at the focal point and in the center of the field) of the first objective lens, imaging by this portion of the lens system is totally free of spherical aberration.
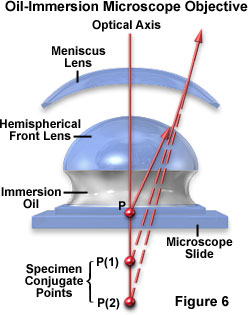
The general design of a practical oil immersion objective includes a hemispherical front lens element, followed by a positive meniscus lens and a doublet lens group. Presented in Figure 6 are the aplanatic refractions that occur at the first two lens elements in a typical apochromatic oil immersion objective. The specimen is sandwiched between the microscope slide and cover glass at point P, the aplanatic point of the hemispherical lens element. Light rays refracted at the rear of the hemispherical lens appear to proceed from point P(1), which is also the center of curvature for the first surface of the meniscus lens. The refracted light rays enter the meniscus lens along the radius of its first surface and experience no refraction at that surface. At the rear surface of the meniscus lens, light rays are refracted aplanatically, so they appear to diverge from point P(2). Refraction of the light rays at the surfaces of subsequent lens groups in the objective complete the convergence of light rays originating from point P, thus forming the intermediate image.
Properly designed oil immersion objective lenses also correct for chromatic defects that are introduced by the first two lens elements, while introducing a minimum amount of spherical aberration. The fact that the light cone is partially converged before entering the first lens element aids in the control of spherical aberration. It should be noted that employing an oil immersion objective without the application oil between the coverslip and first lens element results in defective images. This due to refraction that occurs at the surface of the front lens, which introduces spherical aberration that cannot be corrected by subsequent lens components within the objective.
The advantages of oil immersion objectives are severely compromised if the wrong immersion fluid is utilized. Microscope manufacturers produce objectives with tight tolerances to refractive index and dispersion, which require matching values in the liquid placed between the cover glass and objective front lens. It is advisable to employ only the oil intended by the objective manufacturer, and to not mix immersion oils between manufacturers to avoid unpleasant artifacts such as crystallization or phase separation.
Objectives that use water and/or glycerin as an imaging medium are also available for applications with living cells in culture or sections of tissue immersed in physiological saline solution. Plan apochromat water immersion lenses are equipped with correction collars and numerical apertures up to 1.2, slightly less than their oil immersion counterparts. These objectives allow microscopists to focus through up to 200 microns of aqueous media and still retain excellent optical correction. The downside is that high numerical aperture water immersion lenses often cost many thousands of dollars and the image can still degrade when the objective is focused deeply through refractile tissue or cell parts. For more details on water, glycerin, and oil immersion objectives, visit our section on immersion media in the microscopy primer.
Immersion Oil and Refractive Index

Explore how variations in the refractive index of the imaging medium effect the ability of an objective to capture light rays emanating from the specimen.
Start Tutorial »There is a wealth of information inscribed on the objective barrel, as discussed in our section on specifications and identification of objectives. Briefly, each objective has inscribed on it the magnification (e.g. 10x, 20x or 40x etc.); the tube length for which the objective was designed to give its finest images (usually 160 millimeters or the Greek infinity symbol); and the thickness of cover glass protecting the specimen, which was assumed to have a constant value by the designer in correcting for spherical aberration (usually 0.17 millimeters). If the objective is designed to operate with a drop of oil between it and the specimen, the objective will be engraved OIL or OEL or HI (homogeneous immersion). In cases where these latter designations are not engraved on the objective, the objective is meant to be used dry, with air between the lowest part of the objective and the specimen. Objectives also always carry the engraving for the numerical aperture (NA) value. This may vary from 0.04 for low power objectives to 1.3 or 1.4 for high power oil-immersion apochromatic objectives. If the objective carries no designation of higher correction, one can usually assume it is an achromatic objective. More highly corrected objectives have inscriptions such as apochromat or apo, plan, FL, fluor, etc. Older objectives often have the focal length (lens-to-image distance) engraved on the barrel, which is a measure of the magnification. In modern microscopes, the objective is designed for a particular optical tube length, so including both the focal length and magnification on the barrel becomes somewhat redundant.
Table 2 lists working distance and numerical aperture as a function of magnification for the four most common classes of objectives: achromats, planachromats, planfluorites, and planapochromats. Note that dry objectives all have a numerical aperture value of less than 1.0 and only objectives designed for liquid immersion media have a numerical aperture that exceeds this value.
Objective Specifications by Magnification
| Magnification | Numerical Aperture | Working Distance (mm) |
|---|---|---|
| Achromat | ||
| 4x | 0.10 | 30.00 |
| 10x | 0.25 | 6.10 |
| 20x | 0.40 | 2.10 |
| 40x | 0.65 | 0.65 |
| 60x | 0.80 | 0.30 |
| 100x (oil) | 1.25 | 0.18 |
| Plan Achromat | ||
| 0.5x | 0.02 | 7.00 |
| 1x | 0.04 | 3.20 |
| 2x | 0.06 | 7.50 |
| 4x | 0.10 | 30.00 |
| 10x | 0.25 | 10.50 |
| 20x | 0.40 | 1.30 |
| 40x | 0.65 | 0.57 |
| 50x (oil) | 0.90 | 0.40 |
| 100x (oil) | 1.25 | 0.17 |
| 40x | 0.65 | 0.48 |
| 100x | 0.90 | 0.26 |
| Plan Fluorite | ||
| 4x | 0.13 | 17.10 |
| 10x | 0.30 | 16.00 |
| 20x | 0.50 | 2.10 |
| 40x | 0.75 | 0.72 |
| 40x (oil) | 1.30 | 0.2 |
| 60x | 0.85 | 0.3 |
| 100x (dry) | 0.90 | 0.30 |
| 100x (oil) | 1.30 | 0.20 |
| 100x (oil with iris) | 0.5-1.3 | 0.20 |
| Plan Apochromat | ||
| 2x | 0.10 | 8.50 |
| 4x | 0.20 | 15.70 |
| 10x | 0.45 | 4.00 |
| 20x | 0.75 | 1.00 |
| 40x | 0.95 | 0.14 |
| 40x (oil) | 1.00 | 0.16 |
| 60x | 0.95 | 0.15 |
| 60x (oil) | 1.40 | 0.21 |
| 60x (water immersion) |
1.20 | 0.22 |
| 100x (oil) | 1.40 | 0.13 |
| 100x (NCG oil) | 1.40 | 0.17 |
| NCG = No Cover Glass | ||
Table 2
When a manufacturer's set of matched objectives, e.g. all achromatic objectives of various magnifications (a single subset of the objectives listed in Table 2), are mounted on the nosepiece, they are usually designed to project an image to approximately the same plane in the body tube. Thus, changing objectives by rotating the nosepiece usually requires only minimal use of the fine adjustment knob to re-establish sharp focus. Such a set of objectives is described as being parfocal, a useful convenience and safety feature. Matched sets of objectives are also designed to be parcentric, so that a specimen centered in the field of view for one objective remains centered when the nosepiece is rotated to bring another objective into use.
For many years, objective lenses designed for biological applications from most manufacturers all conformed to an international standard of parfocal distance. Thus, a majority of objectives had a parfocal distance of 45.0 millimeters and were considered interchangeable. With the migration to infinity-corrected tube lengths, a new set of design criteria emerged to correct for aberrations in the objective and tube lenses. Coupled to an increased demand for greater flexibility to accommodate the need for ever-greater working distances with higher numerical apertures and field sizes, interchangeability between objective lenses from different manufacturers disappeared. This transition is exemplified by the modern Nikon CFI-60 optical system that features "Chrome Free" objectives, tube lenses, and eyepieces. Each component in the CFI-60 system is separately corrected without one being utilized to achieve correction for another. The tube length is set to infinity (parallel light path) using a tube lens, and the parfocal distance has been increased to 60 millimeters. Even the objective mounting thread size has been altered from 20.32 to 25 millimeters to meet new requirements of the optical system.
The field diameter in an optical microscope is expressed by the field-of-view number or simply field number, which is the diameter of the viewfield expressed in millimeters and measured at the intermediate image plane. The field diameter in the object (specimen) plane becomes the field number divided by the magnification of the objective. Although the field number is often limited by the magnification and diameter of the ocular (eyepiece) field diaphragm, there is clearly a limit that is also imposed by the design of the objective. In early microscope objectives, the maximum usable field diameter was limited to about 18 millimeters (or considerably less for high magnification eyepieces), but modern planapochromats and other specialized flat-field objectives often have a usable field that can range between 22 and 28 millimeters or more when combined with wide-field eyepieces. Unfortunately, the maximum useful field number is not generally engraved on the objective barrel and is also not commonly listed in microscope catalogs.
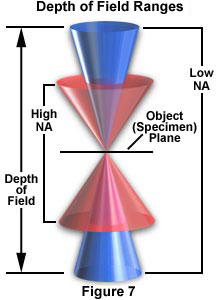
The axial range, through which an objective can be focused without any appreciable change in image sharpness, is referred to as the objective depth of field. This value varies radically from low to high numerical aperture objectives, usually decreasing with increasing numerical aperture (see Table 3 and Figure 7). At high numerical apertures, the depth of field is determined primarily by wave optics, while at lower numerical apertures, the geometrical optical "circle of confusion" dominates. The total depth of field is given by the sum of the wave and geometrical optical depths of field as:
where λ is the wavelength of illumination, n is the refractive index of the imaging medium, NA is the objective numerical aperture, M is the objective lateral magnification, and e is the smallest distance that can be resolved by a detector that is placed in the image plane of the objective. Notice that the diffraction-limited depth of field (the first term on the right-hand side of the equation) shrinks inversely with the square of the numerical aperture, while the lateral limit of resolution is reduced with the first power of the numerical aperture. The result is that axial resolution and the thickness of optical sections are affected by the system numerical aperture much more than is the lateral resolution of the microscope (see Table 3).
Depth of Field and Image Depth
| Magnification | Numerical Aperture | Depth of Field (µm) |
Image Depth (mm) |
|---|---|---|---|
| 4x | 0.10 | 15.5 | 0.13 |
| 10x | 0.25 | 8.5 | 0.80 |
| 20x | 0.40 | 5.8 | 3.8 |
| 40x | 0.65 | 1.0 | 12.8 |
| 60x | 0.85 | 0.40 | 29.8 |
| 100x | 0.95 | 0.19 | 80.0 |
Table 3
The clearance distance between the closest surface of the cover glass and the objective front lens is termed the working distance. In situations where the specimen is designed to be imaged without a cover glass, the working distance is measured at the actual surface of the specimen. Generally, working distance decreases in a series of matched objectives as the magnification and numerical aperture increase (see Table 2). Objectives intended to view specimens with air as the imaging medium should have working distances as long as possible, provided that numerical aperture requirements are satisfied. Immersion objectives, on the other hand, should have shallower working distances in order to contain the immersion liquid between the front lens and the specimen. Many objectives designed with close working distances have a spring-loaded retraction stopper that allows the front lens assembly to be retracted by pushing it into the objective body and twisting to lock it into place. Such an accessory is convenient when the objective is rotated in the nosepiece so it will not drag immersion oil across the surface of a clean slide. Twisting the retraction stopper in the opposite direction releases the lens assembly for use. In some applications (see below), a long free working distance is indispensable, and special objectives are designed for such use despite the difficulty involved in achieving large numerical apertures and the necessary degree of optical correction.
One of the most significant advances in objective design during recent years is the improvement in antireflection coating technology, which helps to reduce unwanted reflections that occur when light passes through a lens system. Each uncoated air-glass interface can reflect between four and five percent of an incident light beam normal to the surface, resulting in a transmission value of 95-96 percent at normal incidence. Application of a quarter-wavelength thick antireflection coating having the appropriate refractive index can decrease this value by three to four percent. As objectives become more sophisticated with an ever-increasing number of lens elements, the need to eliminate internal reflections grows correspondingly. Some modern objective lenses with a high degree of correction can contain as many as 15 lens elements having many air-glass interfaces. If the lenses were uncoated, the reflection losses of axial rays alone would drop transmittance values to around 50 percent. The single-layer lens coatings once utilized to reduce glare and improve transmission have now been supplanted by multilayer coatings that produce transmission values exceeding 99.9 percent in the visible spectral range.
Illustrated in Figure 8 is a schematic drawing of light waves reflecting and/or passing through a lens element coated with two antireflection layers. The incident wave strikes the first layer (Layer A in Figure 3) at an angle, resulting in part of the light being reflected (R(o)) and part being transmitted through the first layer. Upon encountering the second antireflection layer (Layer B), another portion of the light is reflected at the same angle and interferes with light reflected from the first layer. Some of the remaining light waves continue on to the glass surface where they are again both reflected and transmitted. Light reflected from the glass surface interferes (both constructively and destructively) with light reflected from the antireflection layers. The refractive indices of the antireflection layers vary from that of the glass and the surrounding medium (air). As the light waves pass through the antireflection layers and glass surface, a majority of the light (depending upon the incident angle, which is usually perpendicular to the lens in optical microscopy) is ultimately transmitted through the glass and focused to form an image.
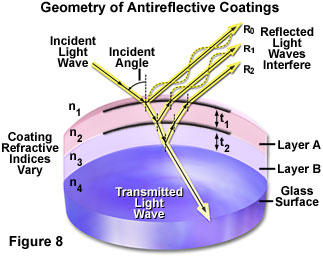
Magnesium fluoride is one of many materials utilized in thin-layer optical antireflection coatings, but most microscope manufacturers now produce their own proprietary formulations. The general result is a dramatic improvement in contrast and transmission of visible wavelengths with a concurrent destructive interference in harmonically-related frequencies lying outside the transmission band. These specialized coatings can be easily damaged by mishandling, and the microscopist should be aware of this vulnerability. Multilayer antireflection coatings have a slightly greenish tint, as opposed to the purplish tint of single-layer coatings, an observation that can be employed to distinguish between coatings. The surface layer of antireflection coatings used on internal lenses is often much softer than corresponding coatings designed to protect external lens surfaces. Great care should be taken when cleaning optical surfaces that have been coated with thin films, especially if the microscope has been disassembled and the internal lens elements are subject to scrutiny.
The focal length of a lens system is defined as the distance from the lens center to a point where parallel rays are focused on the optical axis (often termed the principal focal point). An imaginary plane perpendicular to the principal focal point is called the focal plane of the lens system. Every lens has two principal focal points for light entering each side, one in front and one at the rear. By convention, the objective focal plane that is nearer to the front lens element is known as the front focal plane and the focal plane located behind the objective is termed the rear focal plane. The actual position of the rear focal plane varies with objective construction, but is generally situated somewhere inside the objective barrel for high magnification objectives. Objectives of lower magnification often have a rear focal plane that is exterior to the barrel, located in the thread area or within the microscope nosepiece.
As light rays pass through an objective, they are restricted by the rear aperture or exit pupil of the objective. The diameter of this aperture varies between 12 millimeters for low magnification objectives down to around 5 millimeters for the highest power apochromatic objectives. Aperture size is extremely critical for epi-illumination applications that rely on the objective to act as both an imaging system and condenser, where the exit pupil also becomes an entrance pupil. The image of the light source must completely fill the objective rear aperture to produce even illumination across the viewfield. If the light source image is smaller than the aperture, the viewfield will experience vignetting from uneven illumination. On the other hand, if the light source image is larger than the rear aperture, some light does not enter the objective and the intensity of illumination is reduced.
In conclusion, the development of high quality microscope objectives was ushered by Ernst Abbe, who first developed apochromatic objectives and compensating oculars during the late 1880s in collaboration with Carl Zeiss and Otto Schott. The next major advance in objective design occurred when Hans Boegehold (Zeiss) constructed the first plan achromat and plan apochromat objectives in the late 1930s. More recently, the development of "Chrome Free" (CF) optics by Zenji Wahimoto (Nikon) and Horst Riesenberg (Zeiss) has led to a new revolution in microscope objective design.
Many of the microscope objectives being produced today offer remarkably low degrees of aberration and other imperfections, provided the appropriate objective is selected and it is utilized properly. Nevertheless, the microscopist needs to be aware that objectives are not made to be perfect from every standpoint, but are designed to meet a certain set of specifications depending on intended use, constraints on physical dimensions, and price ranges. Therefore, objectives are made with different degrees of correction for chromatic and spherical aberration, field size and flatness, transmission wavelengths, freedom from fluorescence, birefringence, and other factors contributing to background noise. In addition, they are designed to be used under certain circumscribed conditions, such as with specific tube lengths and tube lenses, type and thickness of immersion media and coverslips, wavelength ranges, field sizes, ocular types, and special condensers. The ultimate goal of the optical microscope is to provide useful magnification that allows minute specimens to be observed in great detail, thus exposing a hidden world of invisible objects that would otherwise remain unseen.
